FastText is an algorithm developed by Facebook that can be used for both word representation and text classification. This post goes through some of the inner workings of the text classifier, in particular how predictions are obtained for a trained model with both n-grams and subword features. The purpose is not to find an optimal model but to bring some clarity to how the algorithm works behind the scenes.

import fasttext
import re
import numpy as np
from collections import Counter

I'm using the same dataset as in the getting started tutorial under Docs -> Text classification on fasttext.cc

with open("cooking.stackexchange.txt", "r") as f:
    raw = f.readlines()

Space is created around special characters and all text is set to lowercase. So "How to clean a cast iron skillet?" becomes "how to clean a cast iron skillet ?". This is more or less the same cleaning as the one in the Docs example.

def process(s):
    s = re.sub(r'([/?!.,;:\-\(\)"])', " \g<0> ", s)
    s = s.lower()

    return s

processed = [process(line) for line in raw]

Here I'm feeding the entire dataset to the algorithm. If you want to build a model that generalises well to new data you should of course consider partitioning it differently.

with open('processed.txt', 'w') as f:
    f.writelines(processed)

Three different models are trained; model_basic, model_subws and model_ngram. The only difference between them are the parameters minn, maxn and wordNgrams.

The ngram model includes bi-grams. In a sentence like "How to clean a cast iron skillet?" we make use of pairs such as (iron, skillet) or (cast, iron). These features can be useful as they might convey more information as a pair than as individual words. They also take order into account, i.e. "iron cast" is not the same as "cast iron".

The subws model breaks down words into substrings with minimun length minn and maximum length maxn. With minn = 2 and maxn = 3 the following subwords are derived from the word skillet: sk, ski, ki, kil, il, ill, ll, lle, le, let and et. These can be used to form new words such as ski, skill and kill. By combining subwords present in training data this way, fastText can create representations of previously unseen words.

model_basic = fasttext.train_supervised(
    input="processed.txt", minn=0, maxn=0, wordNgrams=1)

model_subws = fasttext.train_supervised(
    input="processed.txt", minn=3, maxn=5, wordNgrams=1)

model_ngram = fasttext.train_supervised(
    input="processed.txt", minn=0, maxn=0, wordNgrams=2)

Model architecture

The model architecture is illustrated in the picture below. All input words, \(W_i\), are embedded by the input matrix \(A\) and then averaged together in a vector. That vector is multiplied with output matrix \(B\) and finally softmax is used to assign a probability to each class. The dimension of matrix \(A\) depends on the vocabulary size and the dim parameter. The dimension of matrix \(B\) also depends on dim as well as the the number of distinct classes.

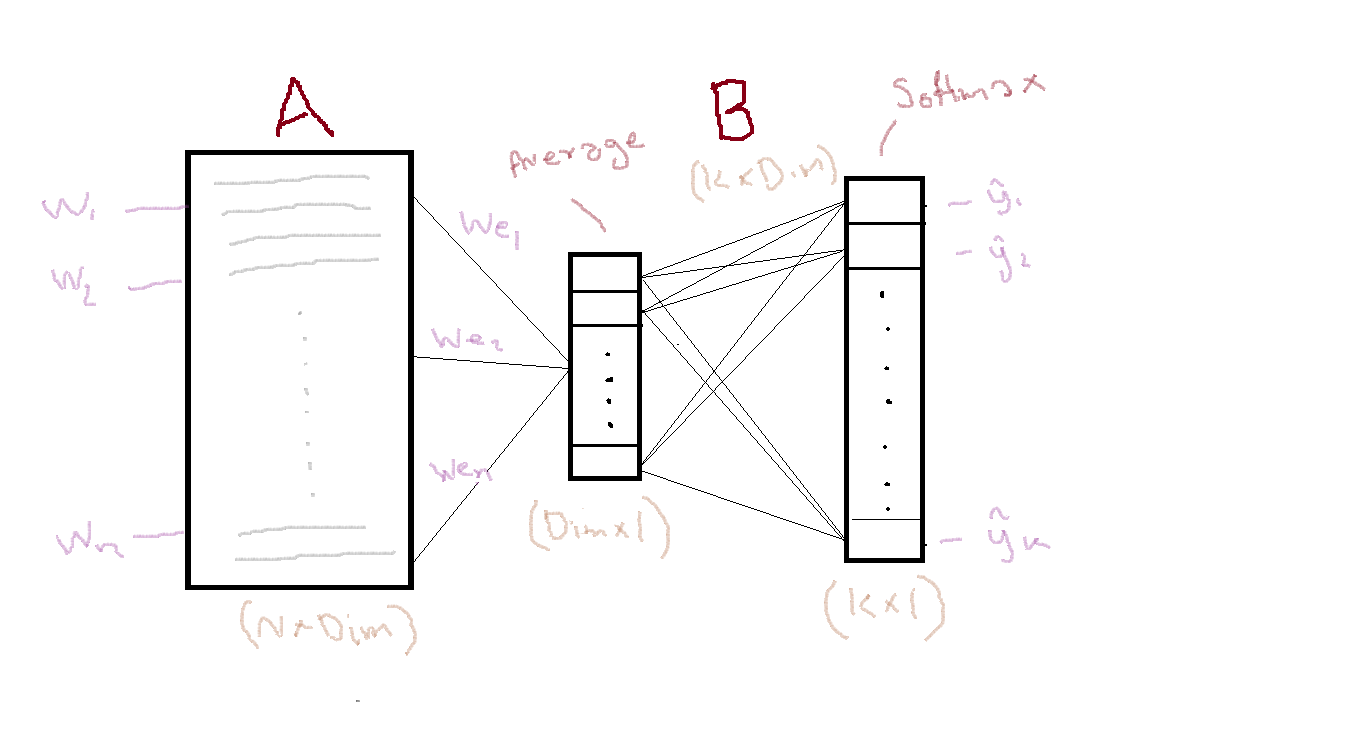
The negative log-likelihood is outlined in the paper $$-\frac{1}{N}\sum_{n=1}^Ny_nlog(f(BAx_n))$$ Here \(x_n\) is a normalized bag of features, i.e. a vector of zeros with word counts in indices for words that are present in the input layer, divided by the total count. So multiplying \(A\) with \(x_n\) gives us the average vector in the picture.

Dimensions of A

The input matrix \(A\) contains vector representations for all words, subwords and n-grams. FastText preallocates space for subwords and n-grams, the size is given by the bucket parameter which defaults to 2e6. The number of rows in \(A\) therefore equals the number of distinct words in the training data plus the bucket size. The model object exposes the input matrix as well as other attributes.

def print_dim(model):
    A = model.get_input_matrix()
    d = str(A.shape)
    n = len(model.words) + model.bucket
    print("input matrix: %14s, words+bucket: %7i, dim: %i" % (d, n, model.dim))

In the basic model the number of rows is equal to the vocabulary size as bucket can be set to zero when there are no subwords or n-grams. For the other models the default bucket size as added to the number of rows. The number of columns is equal to the default value of the dim parameter.

print_dim(model_basic)
print_dim(model_subws)
print_dim(model_ngram)

input matrix:    (8926, 100), words+bucket:    8926, dim: 100
input matrix: (2008926, 100), words+bucket: 2008926, dim: 100
input matrix: (2008926, 100), words+bucket: 2008926, dim: 100

Bag of features

Once a model has been trained all that's needed to calculate a prediction is a bag of features representation of the input data. The function below outlines how this vector can be constructed given the yet to be implemented functions get_word_idx(), get_subword_idx() and get_ngram_idx().

def bag_of_features(s, vocab, minn, maxn, wordNgrams, bucket=int(2e6)):
    tokens = s.split()
    # fastTetxt adds the end of sentence token </s>
    tokens.append('</s>')
    idx = Counter()
    nwords = len(vocab)

    for token in tokens:
        # To be implemented
        token_id = get_word_idx(token, vocab)
        if token_id >= 0:
            idx.update([token_id])

        if maxn > 0 and token != '</s>':
            # To be implmented
            idx.update(get_subword_idx(token, nwords, bucket, minn, maxn))

    if wordNgrams > 1:
        # To be implemented
        idx.update(get_ngram_idx(tokens, nwords, wordNgrams, bucket))

    x = np.zeros((nwords + bucket), dtype=np.float32)
    keys = np.fromiter(idx.keys(), dtype=np.int64)
    values = np.fromiter(idx.values(), dtype=np.float32)
    x[keys] = values / values.sum()

    return x

Hashing

Indices are obtained through hashing. The function get_hash() below is a python implementation of the c++ hashing function in fastText.

def get_hash(token):
    old_settings = np.seterr(all="ignore")
    h = np.uint32(2166136261)
    for char in token:
        char_bytes = char.encode("utf-8")
        for b in char_bytes:
            h = h ^ np.uint32(np.int8(b))
            h = h * np.uint32(16777619)
    np.seterr(**old_settings)

    return h

Words

FastText starts out by preallocating a vector of size 30e6. For each word an index is returned from the hashing function which determines the position in the vector. If a position is already taken the index is incremented until a free slot is found. If the corpus is large, i.e. there are many distinct words in the training data, the preallocated vector will start filling up and finding free positions will be slow. To mitigate this fastText starts pruning once the vocabulary grows bigger than 75% of the preallocated size.

Once the vocabulary is built words are stored in a word vector where they are ordered by descending frequency and indices are updated. FastText adds the end of sentence token </s> at the end of each input line. It is therefore a likely candidate to show in first position.

words = Counter()
for row in processed:
    s = re.sub('__[a-z]+__[a-z]+\s', '', row)
    tokens = s.split() + ['</s>']
    for w in tokens:
        words.update([w])
words = [tup[0] for tup in words.most_common()]

print('Most common: ' + ' '.join(words[:5]))

Most common: </s> ? - to a

The number of distinct words in this dataset is much smaller than the maximum vocabulary size, so no words will be pruned from the vocabulary. This means that the row index of a word in \(A\) is identical to the index in the sorted words vector.

def get_word_idx(token, words):
    try:
        return words.index(token)
    except ValueError:
        return -1

Subwords

The function get_subwords() returns all subwords for a given word and parameters minn and maxn.

def get_subwords(word, minn, maxn):
    word_length = len(word)
    subwords = []

    for i in range(word_length):
        j = i
        n = 1
        s = ""

        while j < word_length and n <= maxn:
            s += word[j]
            j += 1
            if n >= minn and not (n == 1 and (i == 0 or j == word_length)):
                subwords.append(s)
            n += 1

    return subwords

This is the result for the word cake surrounded by begining and end of word tokens <> and minn=2 and maxn=3

get_subwords("<cake>", 2, 3)

['<c', '<ca', 'ca', 'cak', 'ak', 'ake', 'ke', 'ke>', 'e>']

Unlike when building the vocabulary of words, collisions are allowed in the bucket range and more probable if the bucket size is small. The modulo operator makes sure no index exceeds the vector dimensions.

def get_subword_idx(token, nwords, bucket, minn, maxn):
    word = "<" + token + ">"
    subwords = get_subwords(word, minn, maxn)
    idx = []

    for subword in subwords:
        idx.append(nwords + get_hash(subword) % bucket)

    return idx

n-grams

N-grams are also in the bucket range and thus free to collide with subwords. All inputs are first hashed individually. The function then proceeds to loop over all n-grams, in this case bi-grams, adding an additional hash value for each one of them to the list of output indices.

def get_ngram_idx(tokens, nwords, wordNgrams, bucket):
    hashes = []

    for token in tokens:
        hashes.append(get_hash(token))

    idx = []
    hashes_length = len(tokens)

    old_settings = np.seterr(all="ignore")

    for i in range(hashes_length):
        h = np.uint64(np.int32(hashes[i]))
        j = i + 1

        # Loop through all n-grams starting from position i.
        while j < hashes_length and j < i + wordNgrams:
            h = np.uint64(h * np.uint64(116049371))
            h = h + np.uint64(np.int32(hashes[j]))
            h = h % np.uint64(bucket) + np.uint64(nwords)

            idx.append(h)
            j += 1

    np.seterr(**old_settings)

    return idx

Predictions

The predict function makes use of trained matrices \(A\) and \(B\). Predictions are obtained by taking softmax of the output layer.

def predict(bof, model):
    A = model.get_input_matrix()
    B = model.get_output_matrix()
    avg = np.matmul(np.transpose(A), x)
    output = np.matmul(B, avg)
    pred = softmax(output)
    # Rank predictions from high to low
    rnk = pred.argsort()[::-1]

    return pred[rnk]

This is how softmax is implemented in the source code. Note that a small constant value of 1e-5 is added to all predictions.

def softmax(v):
    exp_v = np.exp(v - v.max())
    exp_v_n = exp_v / exp_v.sum()
    y = np.exp(np.log(exp_v_n + 1e-5))

    return y

Using the input sentence "What's the purpose of bread?", a normalised bag of features vector is created for each model. They are multiplied by each models specific weight matrices in the predict function before predictions are returned.

s = "What's the purpose of bread?"

x = bag_of_features(s, vocab=words, minn=0, maxn=0,
                    wordNgrams=0, bucket=0)
preds_basic = predict(x, model_basic)

x = bag_of_features(s, vocab=words, minn=3, maxn=5,
                    wordNgrams=0, bucket=int(2e6))
preds_subws = predict(x, model_subws)

x = bag_of_features(s, vocab=words, minn=0, maxn=0,
                    wordNgrams=2, bucket=int(2e6))
preds_ngram = predict(x, model_ngram)

These are the top eight highest probabilites (there are a total of 669 distinct labels)

print(preds_basic[:8])
print(preds_subws[:8])
print(preds_ngram[:8])

[0.176917 0.097765 0.051303 0.027405 0.027188 0.026402 0.025514 0.024879]
[0.046017 0.039449 0.024450 0.023647 0.022368 0.021683 0.018563 0.013396]
[0.146974 0.069968 0.069439 0.060680 0.023812 0.021596 0.019438 0.017390]

There is, of course, already a predict function on the model object. Let's use it to compare results!

print(model_basic.predict(s, k=-1)[1][:8])
print(model_subws.predict(s, k=-1)[1][:8])
print(model_ngram.predict(s, k=-1)[1][:8])

[0.176916 0.097765 0.051303 0.027405 0.027188 0.026402 0.025514 0.024879]
[0.046017 0.039449 0.024450 0.023647 0.022368 0.021683 0.018563 0.013396]
[0.146974 0.069968 0.069439 0.060680 0.023812 0.021596 0.019438 0.017390]

They are identical so the bag of features vector implementation above seems correct.

One last no not ot ote te

Imagine the model encounters a previously unseen word, i.e. a word that is not in the training data. Neither the basic nor the n-gram model would produce a meaningfull representation as it doesn't map to any row in \(A\).

print(get_word_idx("castiron", words))

-1

But in the subwords model "castiron" is broken down to a range of different subwords, as explained above, among others 'cast' and 'iron'.

print(get_subwords("castiron", minn=3, maxn=5))

['cas', 'cast', 'casti', 'ast', 'asti', 'astir', 'sti', 'stir', 'stiro', 'tir', 'tiro', 'tiron', 'iro', 'iron', 'ron']

These will all be hashed and receive an index in the bucket range and therby get a numerical representation. This might, or might not, produce a better model.

Summary

The fastText model object exposes functions similar to the once implemented in this post. The average vector is e.g. returned by get_sentence_vector(). Hopefully, this walkthrough brings some clarity to some of the details of the implementation and how the algorithm works.

There are arguments additional to the once mentioned in this post that will have an effect on training and prediction. The sampling threshold tcan be modified, a different loss function loss can be specified etc.

FastText can be trained with pretrainedVectors, i.e. an input matrix with pretrained weights. The vocabluary can still grow, given that the maximum size is not reached, but the dimension argument dim has to be identical to the dimension of the provided input matrix. In the bucket range everything works as before. This might be especially helpfull if your dataset is small and what's more fasttext.cc provides several pretrained models for a range of different languages.

With the use of the autotune module fastText is an easy and quick way to get good results. I recommend visiting fasttext.cc, reading the text classification paper and trying it out!